Фибоначчи

Леонардо Фибоначчи (итал. Leonardo Fibonacci; 1170 – 1250) – итальянский математик из города Пиза, считающийся одним из самых выдающихся западных математиков XIII века. Настоящее имя Леонардо Пизанский.

Имя, которым обычно называют Фибоначчи, было придумано в 1838 году франко-итальянским историком Гийомом Либри и является сокращением от filius Bonacci (сын Боначчи). Сам Леонардо называл себя Леонардо Биголло Пизано (Леонардо путешественник из Пизы).

Благодаря своей книге Liber Abaci (Книга расчетов), написанной им в 1202 и 1220 (второе издание) годах, Леонардо Фибоначчи популяризировал в западном мире индуистско-арабскую систему счисления. Он также познакомил Европу с последовательностью чисел Фибоначчи, которую использовал в качестве примера в Liber Abaci.

Биография Леонардо Фибоначчи

Леонардо Пизанский родился примерно в 1170 году в семье итальянского купца и таможенного чиновника Гульельмо. Отец Леонардо руководил торговым постом в Беджае (Алжир). В детстве мальчик много путешествовал с отцом по странам Северной Африки, где познакомился с индийско-арабской системой счисления.

В своих путешествиях Леонардо Пизанский встречался со многими торговцами и изучал их арифметические системы. Вскоре он осознал преимущества индийско-арабской системы, которая в отличие от римских цифр, использовавшихся в то время, позволяла легко вычислять с использованием позиционной системы счисления. В 1202 году он завершил свою рукопись Liber Abaci (Книга абака или Книга расчетов), которая популяризировала индийско-арабские цифры в Европе.

Леонардо Пизанский стал гостем императора Фридриха II, который увлекался математикой и наукой. В 1240 году Пиза чествовала Фибоначчи (именуемого Леонардо Биголло), предоставив ему жалованье в указе, который признавал его заслуги, оказанные городу в качестве советника по вопросам бухгалтерского учета и обучения граждан.

Статуя Леонардо Фибоначчи

В Пизе, в монастыре исторического кладбища Кампо-Санто, находится статуя Леонардо Пизанского с надписью “A Leonardo Fibonacci Insigne Matematico Pisano del Secolo XII”. Портрет Фибоначчи является продуктом фантазии скульптора, поскольку до нашего времени не сохранилось изображений великого математика.

С инициативой создания статуи 23 сентября 1859 года выступили два члена правительства великого Герцогства Тоскана, Беттино Рикасоли и Козимо Ридольфи, которые издали указ о финансировании работ по созданию памятника великому математику. Изготовить скульптуру было поручено флорентийскому скульптору Джованни Пагануччи, который завершил работу в 1863 году. Статуя была установлена в Пизе на кладбище Кампо-Санто, где погребальные памятники пизанских граждан вместе с древними саркофагами и произведениями искусства образуют уникальный мемориальный ансамбль.

В 1944 году во время Второй мировой войны, в боях за Пизу, статуя была повреждена. В 1950-х годах она была восстановлена и установлена в парке Джардино-Скотто у восточного входа в Старый город. В 1990-х годах Пизанская городская администрация решила вернуть статую на прежнее место в Кампо-Санто.

Книга Liber Abaci

В Liber Abaci (выпуск 1202 года) Леонардо Пизанский ввел так называемый modus Indorum (метод индусов), известный сегодня как индуистско-арабская система счисления. Книга пропагандирует нумерацию с цифрами 0-9 и позиционную систему счисления. Книга продемонстрировала удобство индуистско-арабской системы счисления, применив новые цифры к учету товаров, преобразованию мер и весов, расчету процентов, обмену денег. Книга была хорошо принята в образованной Европе и оказала глубокое влияние на европейскую мысль. Копий издания 1202 года не существует.

В первом разделе издания 1228 года вводится индуистско-арабская система счисления и сравнивается с другими системами, такими как римские цифры, и методы преобразования других систем счисления в индуистско-арабские цифры. Замена римской системы счисления, ее древнеегипетского метода умножения и использования счетных досок для расчетов, на индуистско-арабскую систему счисления позволили упростить и ускорить деловые расчеты, что привело к росту банковского дела и бухгалтерского учета в Европе.

Во втором разделе объясняется использование индуистско-арабских цифр в бизнесе, например, конвертация различных валют, расчет прибыли и вычисление процентов, которые были важны для растущей банковской отрасли. В книге также рассматриваются иррациональные и простые числа.

Последовательность Фибоначчи

В 12 главе Liber Abaci описывается задача, связанная с ежемесячным ростом популяции кроликов. Имеется пара кроликов, которая раз в месяц производит на свет другую пару кроликов. Родившаяся пара кроликов через два месяца произведет на свет еще одну пару кроликов. Через год кроликов будет 233 пары. Числовая последовательность пар кроликов позже была названа “числа Фибоначчи” или “бесконечность Фибоначчи”:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …

Хотя Liber Abaci содержит самое раннее известное описание последовательности за пределами Индии, последовательность была описана индийскими математиками еще в шестом веке.

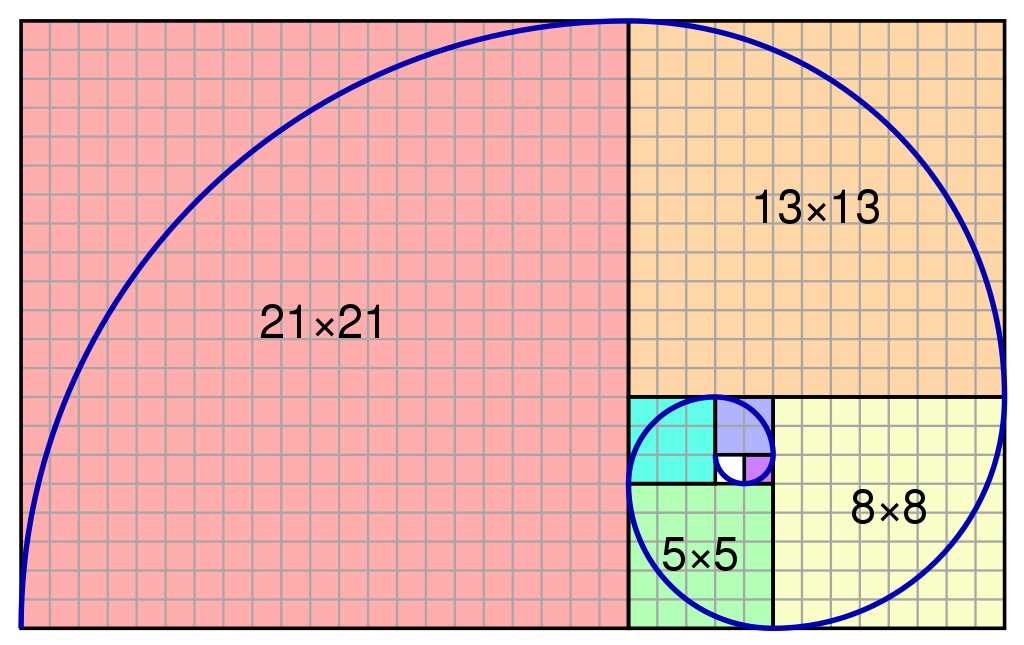
В последовательности чисел Фибоначчи каждое последующее число является суммой двух предыдущих чисел. Леонардо Пизанский опустил ноль, используемый в наше время, и начал последовательность с единицы: 1, 1, 2, 3, 5, 8 … .

Особенностью ряда чисел Фибоначчи является то, что с ростом числовых значений, деление следующего числа на предыдущее приближается к коэффициенту 1,618. Этот коэффициент считается самым гармоничным соотношением двух величин и подробно описывается в трудах Евклида и Леонардо да Винчи как “Золотое сечение”.

Путем несложных вычислений можно получить коэффициенты 0.236, 0.382, 0.618, 1.618, 2.618, 4.236. Эти коэффициенты применяются в науке, искусстве, медицине. Многие природные явления развиваются по коэффициентам Fibonacci.

Основываясь на коэффициентах Фибоначчи, в трейдинге применяют уровни Фибоначчи: 23,6%, 38,2%, 50%, 61,8%, 100%, 161,8%, 261,8%, 423,6%. Эти числа использовал Ральф Нельсон Эллиотт в своей торговой стратегии “Волны Эллиотта”, которая является одной из самых известных стратегий торговли на фондовом рынке.

Вычисление уровней Фибоначчи

Последовательность чисел Фибоначчи используется в биржевой торговле для получения уровней коррекций и уровней расширения Фибоначчи. Коррекции измеряют откаты внутри тренда, в то время как расширения показывают, как далеко может зайти импульсная волна по направлению тренда.

Если цена акции растет с 50 до 100 руб., а затем снижается до 75 руб., то движение от 100 до 75 руб. является коррекцией. Если цена снова начнет расти и достигнет 160 руб., то это будет расширение.

Уровни коррекции и расширения получены из числового ряда Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987… . За исключением первых чисел последовательности, деление предыдущего числа на следующее число равно 0,618 или 61,8%. Разделив число на второе число, справа от него, получим результат 0,382 или 38,2%. Если разделить следующее число на предыдущее, то результат будет равен 1,618 или 161,8%. Если разделить число на второе число слева, результат будет равен 2,618, на третье число слева, результат будет равен 4,236.

Все соотношения, используемые на фондовом рынке, кроме уровней 50% и 100% (поскольку это не официальные уровни коррекции), получаются с помощью умножения и деления цифр из числового ряда Фибоначчи.

Уровни коррекции

Для построения уровней коррекции Фибоначчи необходимо выбрать на графике две точки (локальный минимум и локальный максимум цены). Уровни коррекции находятся между выбранными точками в процентах от этого расстояния.

Пример:

Акции растут с 150 до 200 руб., уровень коррекции 23,6% равен 188,2 руб. (200 – (50 x 0,236) = 188,2). Уровень коррекции 50% равен 175 руб. (150 – (50 x 0,5) = 175).

Уровни расширения

Для построения уровней расширения Фибоначчи необходимо выбрать на графике три точки: начала движения (локальный минимум), конца движения (локальный максимум) и точки между ними (окончание коррекции).

Пример:

Если цена поднимается от 30 руб. (локальный минимум) до 40 руб. (локальный максимум), то уровень 161,8% будет на 16,18 руб. (1,618 x 10 руб.) выше цены, выбранной для третьей точки. Если точка три равна 35 руб., то уровень расширения 161,8% равен 51,18 руб. (35 руб. + 16,18 руб.).

Использование уровней Фибоначчи в трейдинге

Уровни Фибоначчи помогают установить цели движения цены или найти прогнозируемые области поддержки и сопротивления.

К основным уровням, используемым в трейдинге, относятся: 23.6%, 38.2%, 50%, 61.8%, 78.6%, 100%, 161.8%, 261.8%, 423.6%.

Эти соотношения применяются в различных технических индикаторах, использующих коэффициенты Фибоначчи:

• Коррекции Фибоначчи – горизонтальные линии на графике, которые указывают на области поддержки и сопротивления.
• Расширения Фибоначчи – горизонтальные линии на графике, которые указывают, куда может дойти сильная импульсная волна.
• Дуги Фибоначчи – дугообразные линии, построенные относительно локального максимума или минимума, которые представляют собой области поддержки и сопротивления.
• Веера Фибоначчи – диагональные линии, созданные с использованием максимума и минимума, которые представляют собой области поддержки и сопротивления.
• Временные зоны Фибоначчи – вертикальные линии, отложенные в будущее, предназначенные для предсказания того, когда произойдут основные движения цены.

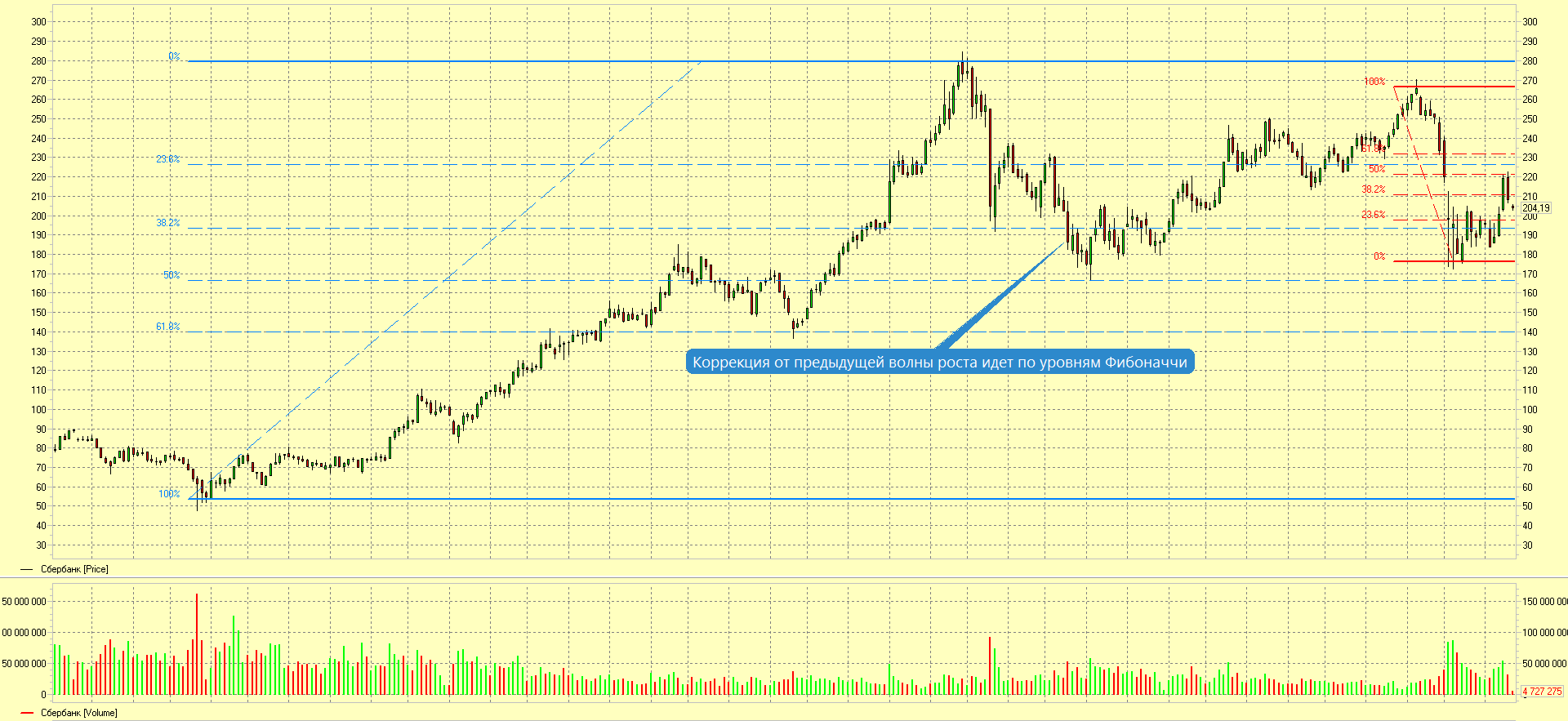Коррекции Фибоначчи являются наиболее распространенными формами технического анализа, основанными на последовательности Фибоначчи. Во время тренда можно использовать коррекции, чтобы определить, насколько глубоким может быть откат. Импульсные волны – более крупные волны по направлению тренда, в то время как откаты – это более мелкие волны в противоположную от импульсных волн сторону. Так как они являются меньшими волнами, они будут составлять процент от большей волны.

Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться назад в направлении тренда, у трейдера появится возможность совершить сделку по направлению основного тренда. Трейдеры заранее не знают, какой уровень будет разворотным, поэтому необходимо дождаться уровня, на котором остановится и развернется цена, прежде чем заключать сделку.

Дуги, веера, расширения и временные зоны показывает потенциальные области поддержки или сопротивления, основанные на числах Фибоначчи, относительно предыдущих движений цены. Эти уровни поддержки или сопротивления можно использовать для прогнозирования целей, где цена может развернуться в обратную сторону.

Расширения Фибоначчи можно использовать на любом рынке и на любом таймфрейме. Поскольку уровни расширения могут быть нарисованы на разных таймфреймах, необходимо искать области, где несколько уровней из разных волн сходятся на одной цене. Этот уровень может быть очень важной областью, в которой произойдет разворот цены.

Стратегии, основанные на числах Фибоначчи

Поскольку трейдеры выбирают на графиках цен локальные максимумы и минимумы, основываясь исключительно на своем опыте, торговля по уровням Фибоначчи является субъективной стратегией. Результаты торговли зависят от того, какие максимумы и минимумы будут выбраны на графике цены.

Нет гарантий того, что цена достигнет уровня или развернется на нем. Цена может легко пройти через несколько уровней или не достичь ни одного из них.

Поэтому коэффициенты Фибоначчи не должны быть единственным фактором, определяющим, покупать или продавать акции. При выработке торговых решений рекомендуется использовать уровни Фибоначчи вместе с другими индикаторами и методами технического анализа. Особенно хорошие результаты дают стратегии, основанные на волнах Эллиотта.

Торговые сигналы в Telegram канале https://erenbur.ru/strategies/torgovye-signaly-v-telegram